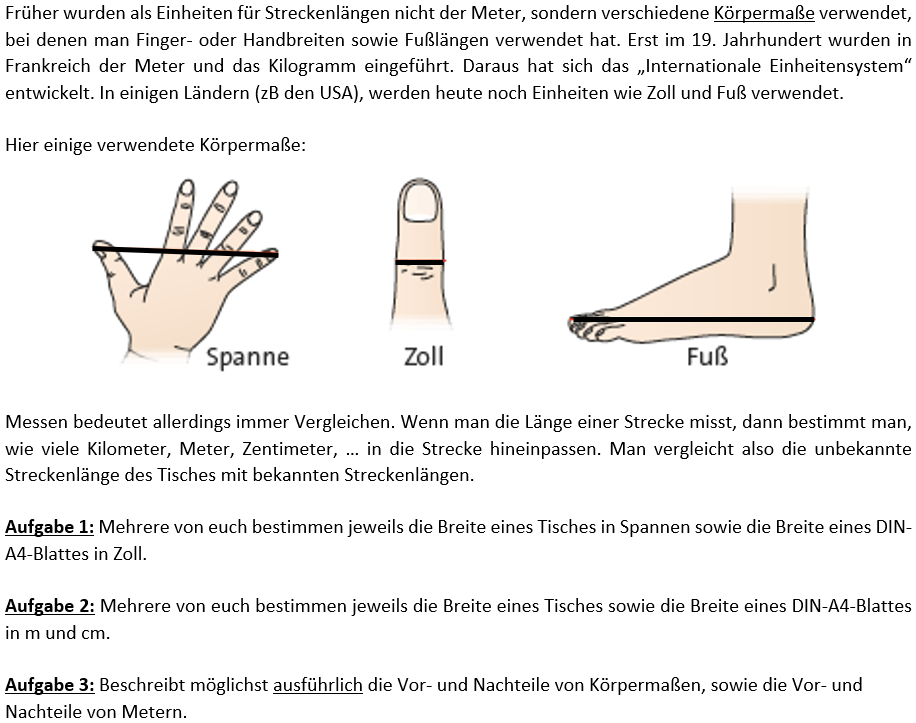
Mindmap
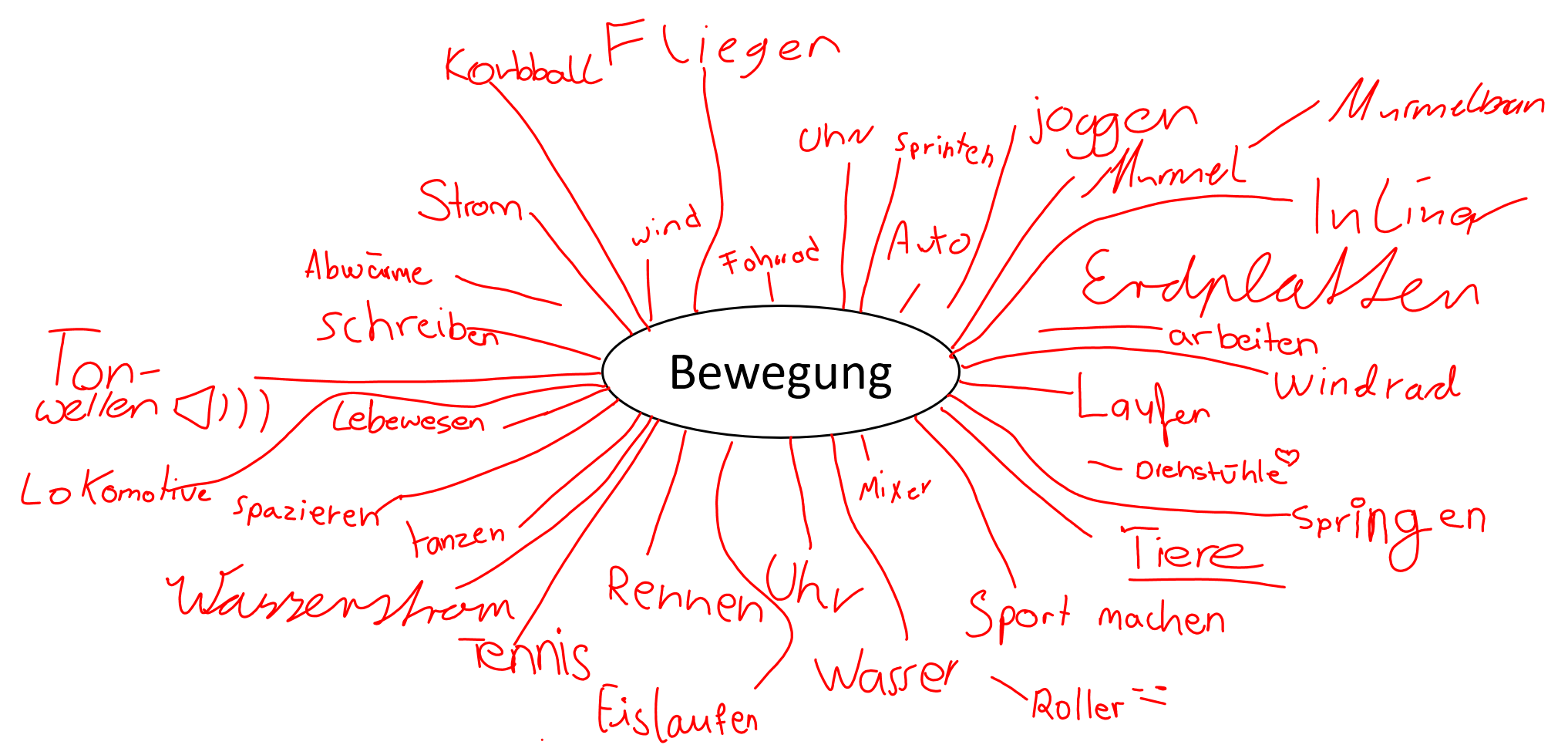
Geschwindigkeit beschreibt man, indem man eine Längeneinheit nennt und sagt, in welcher Zeit man sie durchquert.
Z.B. 1 km/h bedeutet 1 Kilometer in einer Stunde.
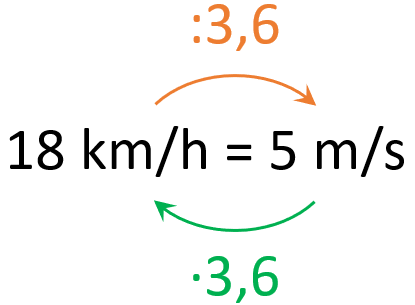
Das liegt daran, dass eine Stunde 3.600 Sekunden hat.
Aufgabe 1: Wie hoch ist die Geschwindigkeit jeweils in m/s und wie hoch in km/h?
a) Ein Jogger legt eine Strecke von 5.000 m in 25 Min. zurück.
b) Der ICE fährt die 286km von Hamburg bis nach Berlin in 1 Stunde und 33 Minuten.
c) Ein Auto fährt 300 km in 2 Stunden und 19 Minuten.
Aufgabe 2:Rechne die Werte in m/s um und ordne sie nach der Größe.
- Schall: 1224 km/h
- Regentropfen: 9 m/s
- Fußball: 100 km/h
- Erde um die Sonne: 30 km/s
Aufgabe 3: Eine australische Rennschnecke bewegt sich mit der Geschwindigkeit 438 km/a (a bedeutet Jahr). Rechne diese Geschwindigkeit auf die Einheit m/h um.
Expertenaufgabe: Ein Motorradfahrer fährt 493 km weit mit einer Durchschnittsgeschwindigkeit von 80 km/h. Wie lange ist er unterwegs?
Nicht spicken!
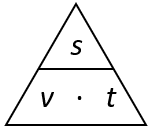
Die Formel v = s/t kann man mit dem Zuhälter-Dreieck verwenden. Der Bruchstrich steht für "geteilt durch". Man hält dann die gesuchte Größe mit dem Finger zu und sieht die Rechnung.


Immer noch nicht spicken!
t-v-Diagramm steht für Zeit-Geschwindigkeits-Diagramm. Das heißt, dass die x-Werte eine Zeitangabe sind und die y-Werte die jeweilige Geschwindigkeit zu der Zeit angeben.
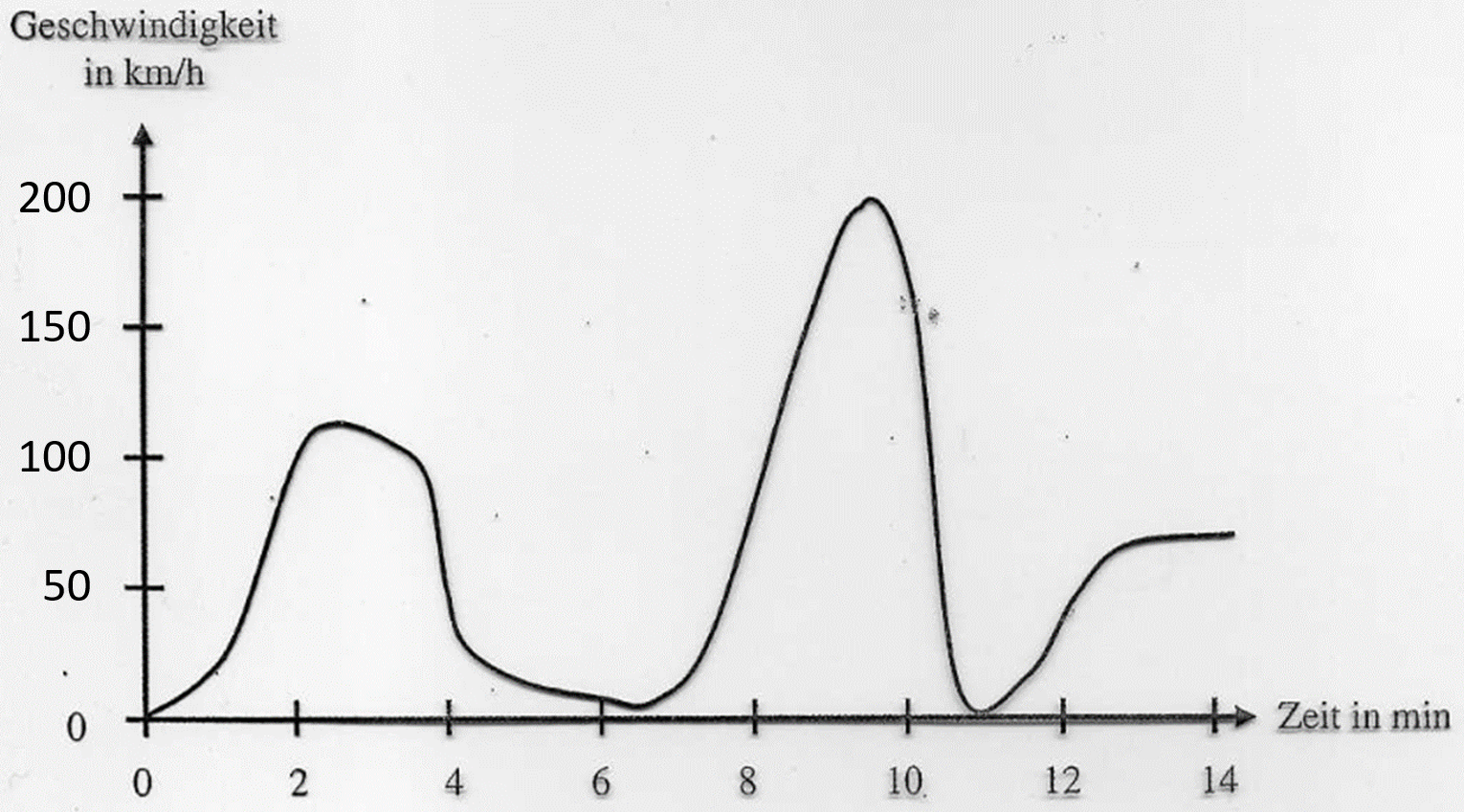
(Anstatt "Zeit" könnte man auch einfach "t" und anstatt "Geschwindigkeit" einfach "v" schreiben.)
Es könnte das Diagramm einer Autofahrt sein. Zu Beginn steht das Auto mit einer Geschwindigkeit von 0. Dann fährt es los, beschleunigt schnell und fährt für ca. 2 Minuten auf einer Landstraße mit 100-110 km/h. Dann kommt es auf eine Ampel zu, bremst stark und rollt langsam darauf zu. Anschließend beschleunigt es starkt, während es auf eine Autobahn fährt. Dort fährt es mit 200 km/h. Es muss eine Vollbremsung machen, um nicht in einen Unfall zu geraten. Danach fährt es lieber langsam mit ca. 70 km/h weiter.
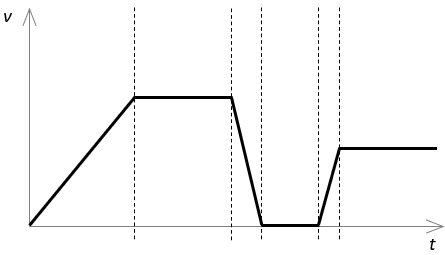
Ordne dem Verlauf im Diagramm die Geschwindigkeitsänderungen zu. Skizziere es dazu ab und trage in den Bereichen zwischen den gestrichelten Linien die Buchstaben A bis F ein.
A Langsames Fahren mit einer konstanten Geschwindigkeit.
B Langsames beschleunigen. Die Geschwindigkeit nimmt zu.
C Eine Weile stehenbleiben.
D Schnelles Fahren mit einer konstanten Geschwindigkeit.
E Bremsen. Die Geschwindigkeit nimmt ab.
F Schnelles beschleunigen. Die Geschwindigkeit nimmt schnell zu.
Denke dir eine Bewegung (z.B. Auto- oder Radfahrt) mit verschiedenen Geschwindigkeiten aus. Beschreibe die Fahrt mit einer kurzen und möglichst kreativen Geschichte und skizziere dazu ein passendes t-v-Diagramm.
Damit es einfacher zu rechnen ist: Immer in m (Meter), s (Sekunden) und m/s (Meter pro Sekunde) rechnen!